gamma_bayes

Fitting the gamma distribution with Bayesian inference

Function to fit the gamma distribution with BayesianMCMC method

Usage

gamma_bayes(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
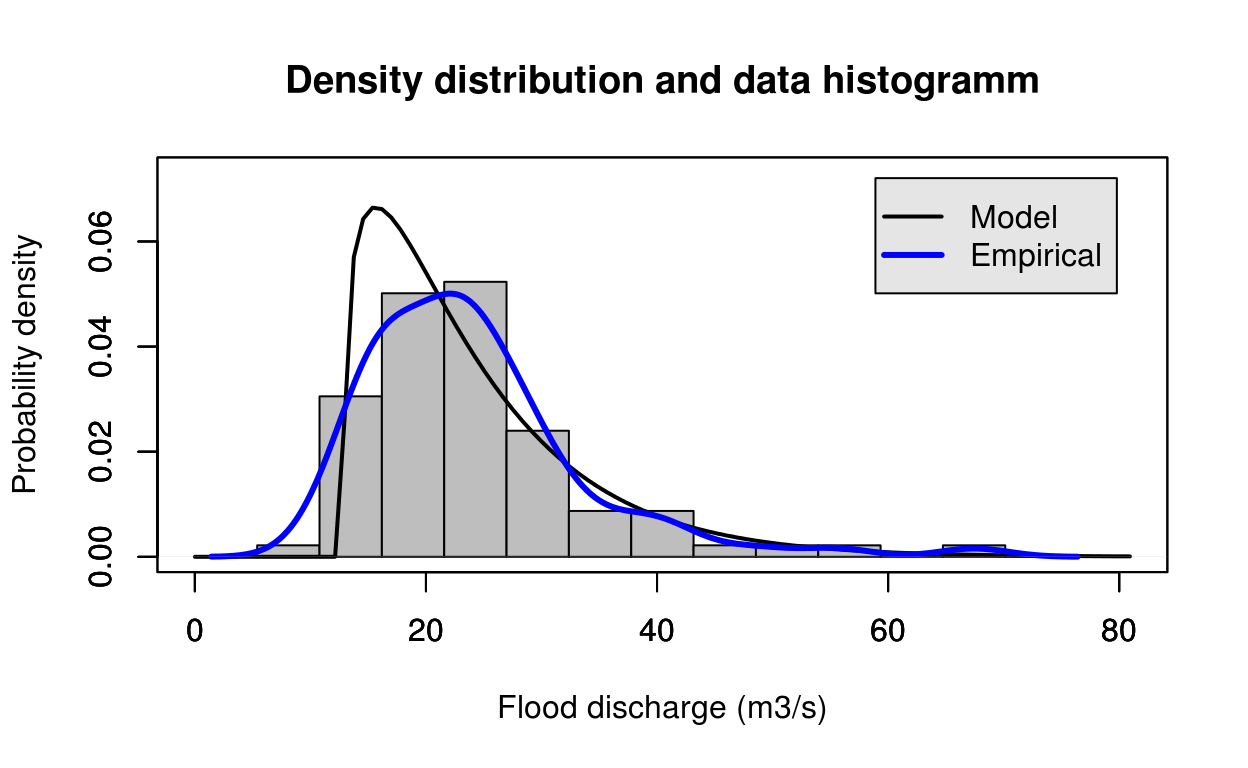
estimate = gamma_bayes(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 5)

## Warning in max(na.omit(y)): no non-missing arguments to max; returning -Inf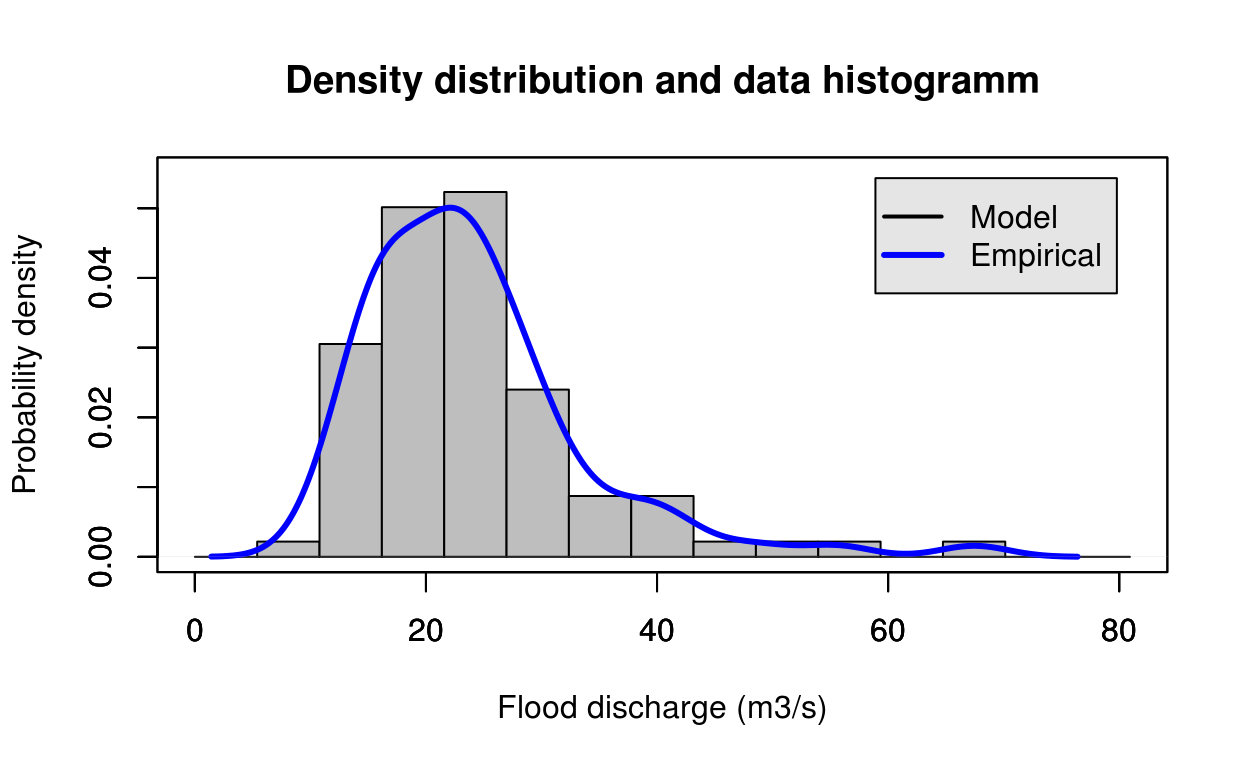

gamma_Lmom

Fitting the gamma distribution with Lmom

Function to fit the gamma distribution with the linear moment method

Usage

gamma_Lmom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters (2) and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gamma_Lmom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 2)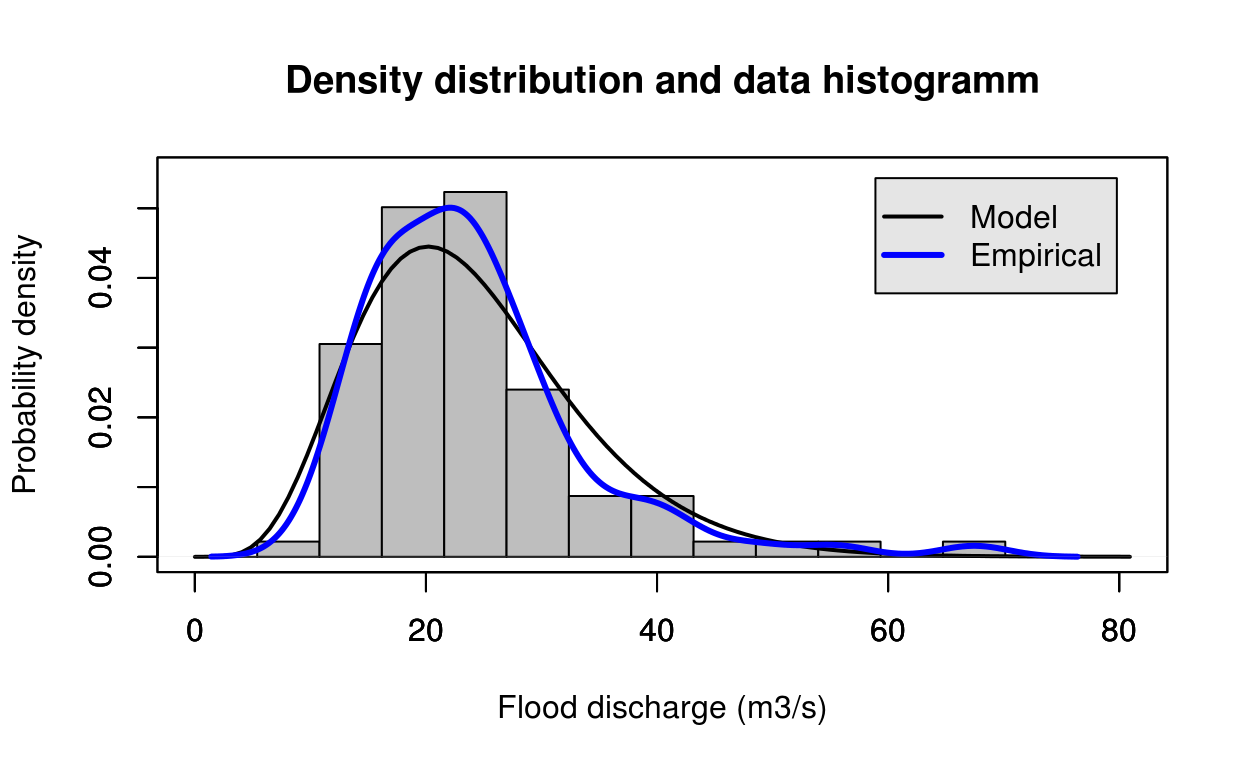

gamma_mle

Fitting the gamma distribution with MLE

Function to fit the gamma distribution with the maximum likelihood method

Usage

gamma_mle(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters (2) and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gamma_mle(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 2)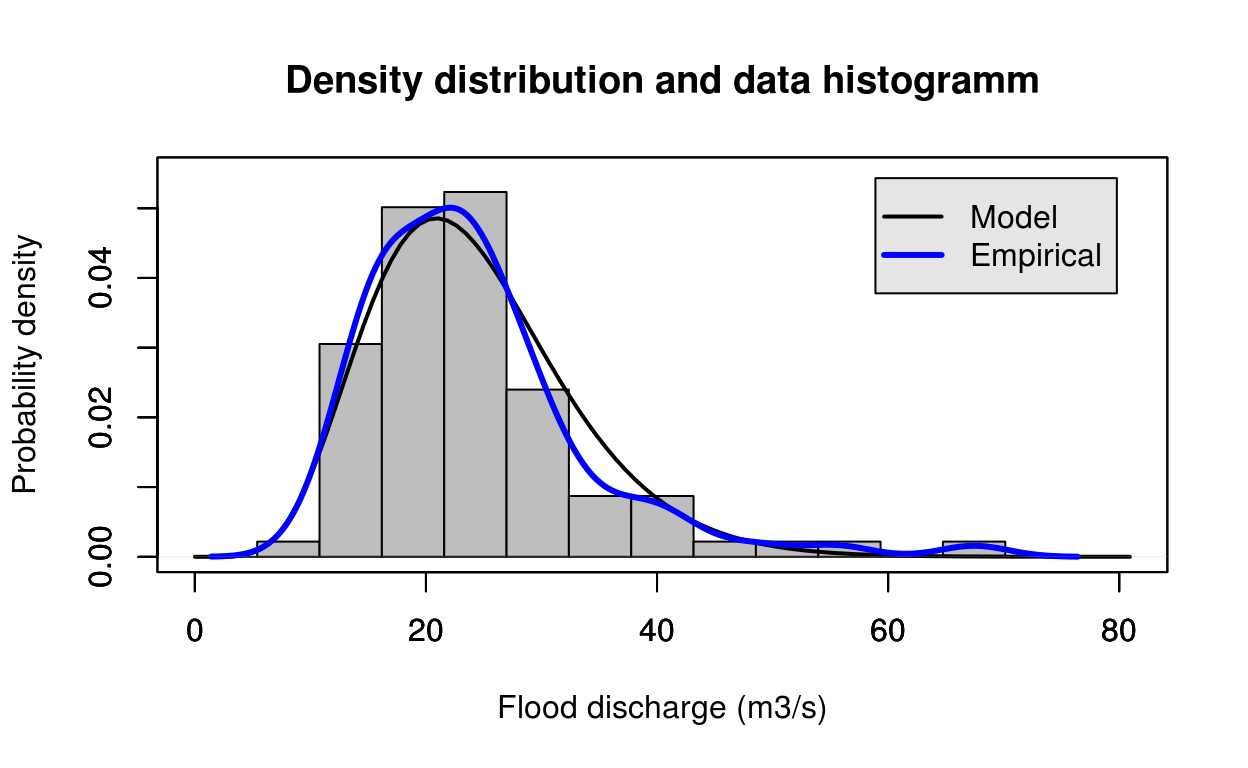

gamma_mom

Fitting the gamma distribution with mom

Function to fit the gamma distribution with the ordinary moments method

Usage

gamma_mom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters (2) and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gamma_mom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 2)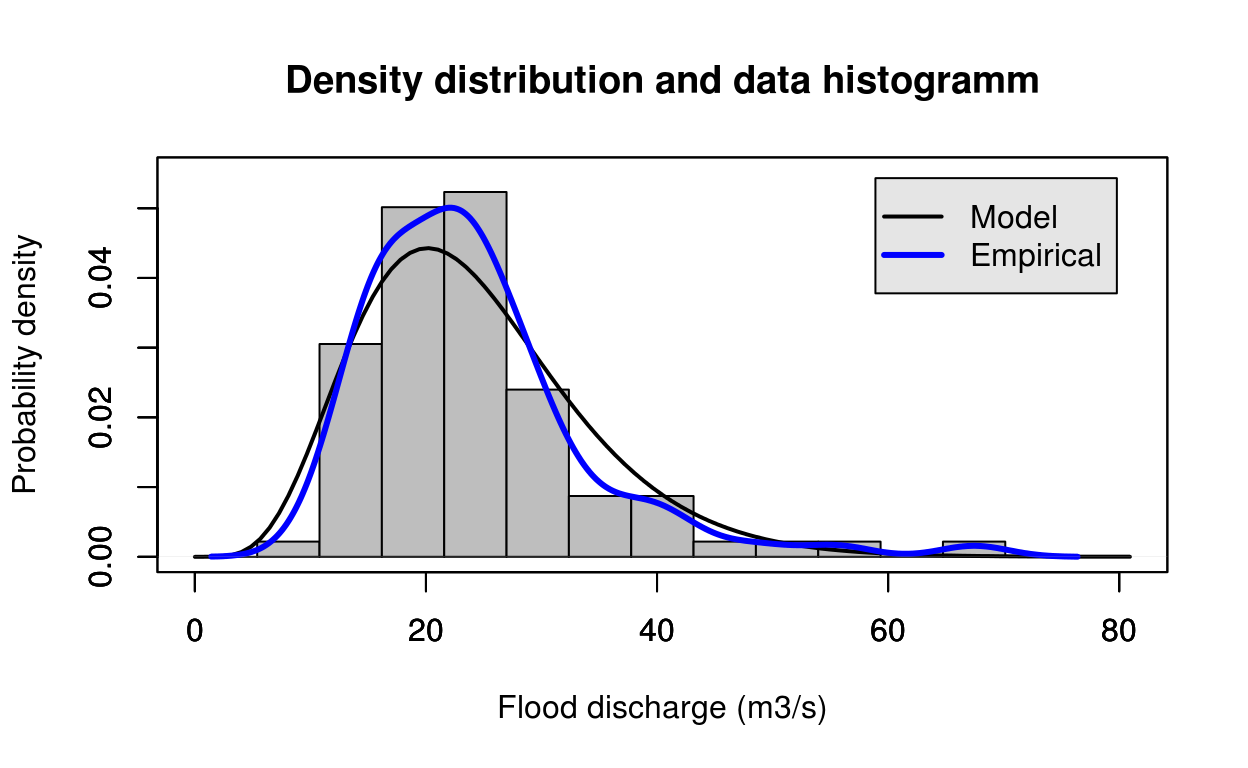

get_posterior_gev

Calculating the posterior predictive distribution

Function to calculate the posterior predictive distribution after calling gev_bayes

Usage

get_posterior_gev(mmrp, mupars, spars, kpars)

Arguments

(mmrp,

mupars, spars, kpars) parameters returned by gev_bayes. mupars, spars, kpars are the ensemble of param$estimate

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

get_posterior_gl

Calculating the posterior predictive distribution for GL

Function to calculate the posterior predictive distribution after calling gev_bayes

Usage

get_posterior_gl(mmrp, mupars, spars, kpars)

Arguments

(mmrp,

mupars, spars, kpars) parameters returned by gev_bayes. mupars, spars, kpars are the ensemble of param$estimate

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

get_posterior_gumbel

Calculating the posterior predictive distribution

Function to calculate the posterior predictive distribution after calling gumbel_bayes

Usage

get_posterior_gumbel(mmrp, mupars, spars)

Arguments

(mmrp,

mupars, spars) parameters returned by gumbel_bayes. mupars, spars are the ensemble of param$estimate

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

get_posterior_PEARSON

Calculating the posterior predictive distribution

Function to calculate the posterior predictive distribution after calling pearson_bayes

Usage

get_posterior_PEARSON(mmrp, mupars, spars, kpars)

Arguments

(mmrp,

mupars, spars, kpars) parameters returned by pearson_bayes. mupars, spars, kpars are the ensemble of param$estimate

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

gev_bayes

Fitting the GEV distribution with Bayesian inference

Function to fit the GEV distribution with BayesianMCMC method WE assume that the shape parameter only has a prior with mean zero and standard deviation 0.2 (dnorm(x[3], 0, 0.2))

Usage

gev_bayes(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gev_bayes(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 3)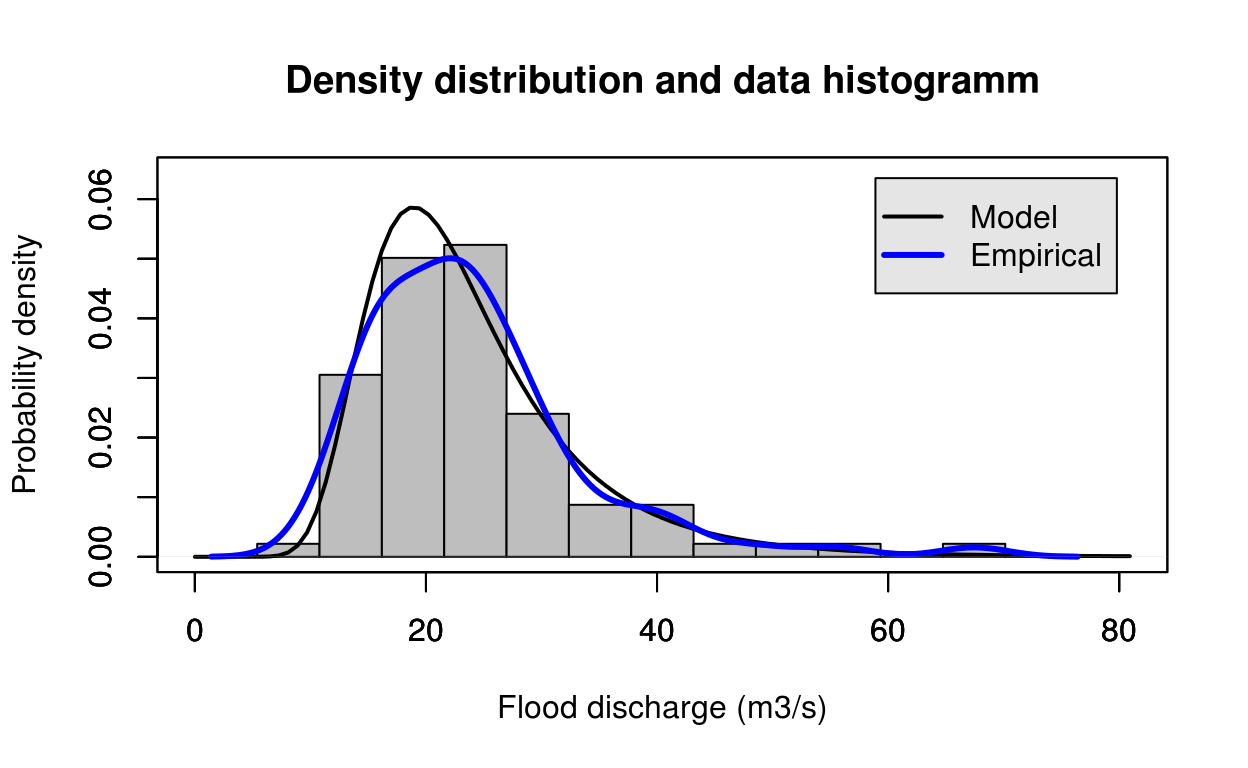

gev_Lmom

Fitting the GEV distribution with Lmom

Function to fit the GEV distribution with the linear moment method

Usage

gev_Lmom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se). Standard error is not yet implemented

Examples

library(FlomKartShinyApp)
estimate = gev_Lmom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 3)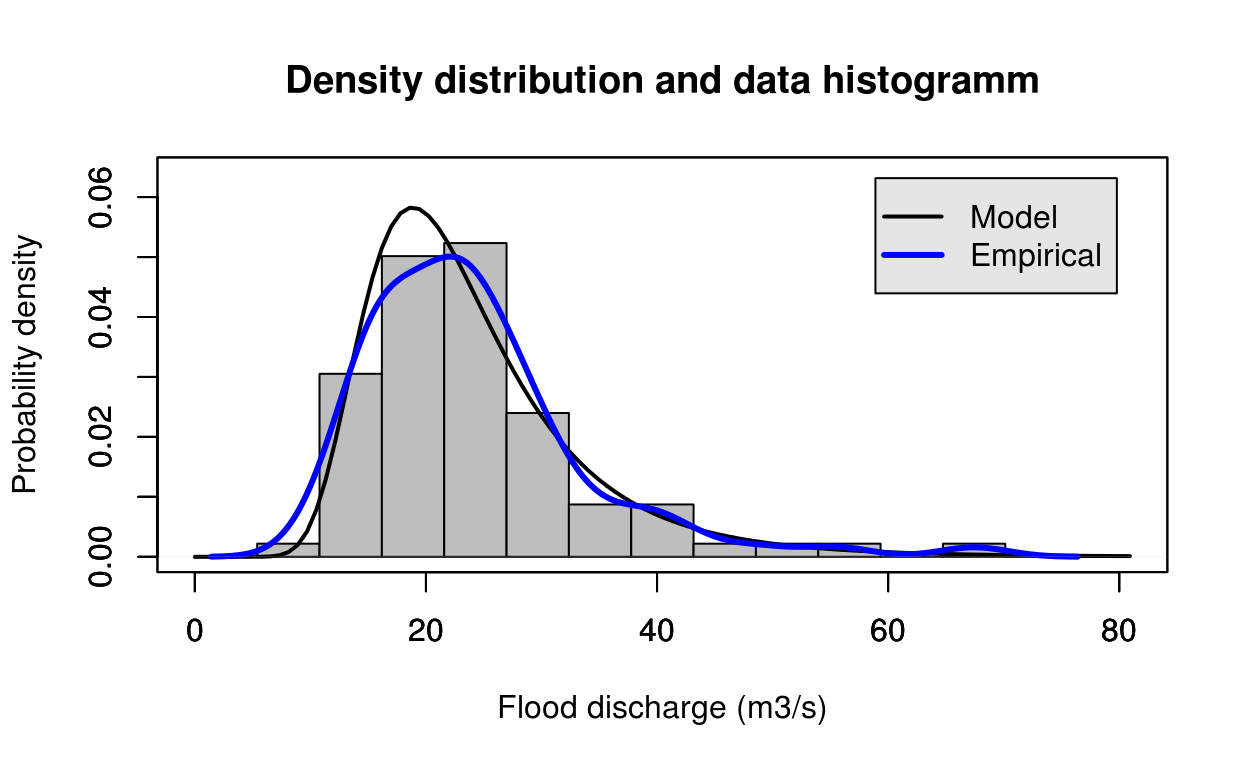

See also

gev_mle, gev_mom

gev_mle

Fitting the GEV distribution with MLE

Function to fit the GEV distribution with the maximum likelihood method

Usage

gev_mle(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gev_mle(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 3)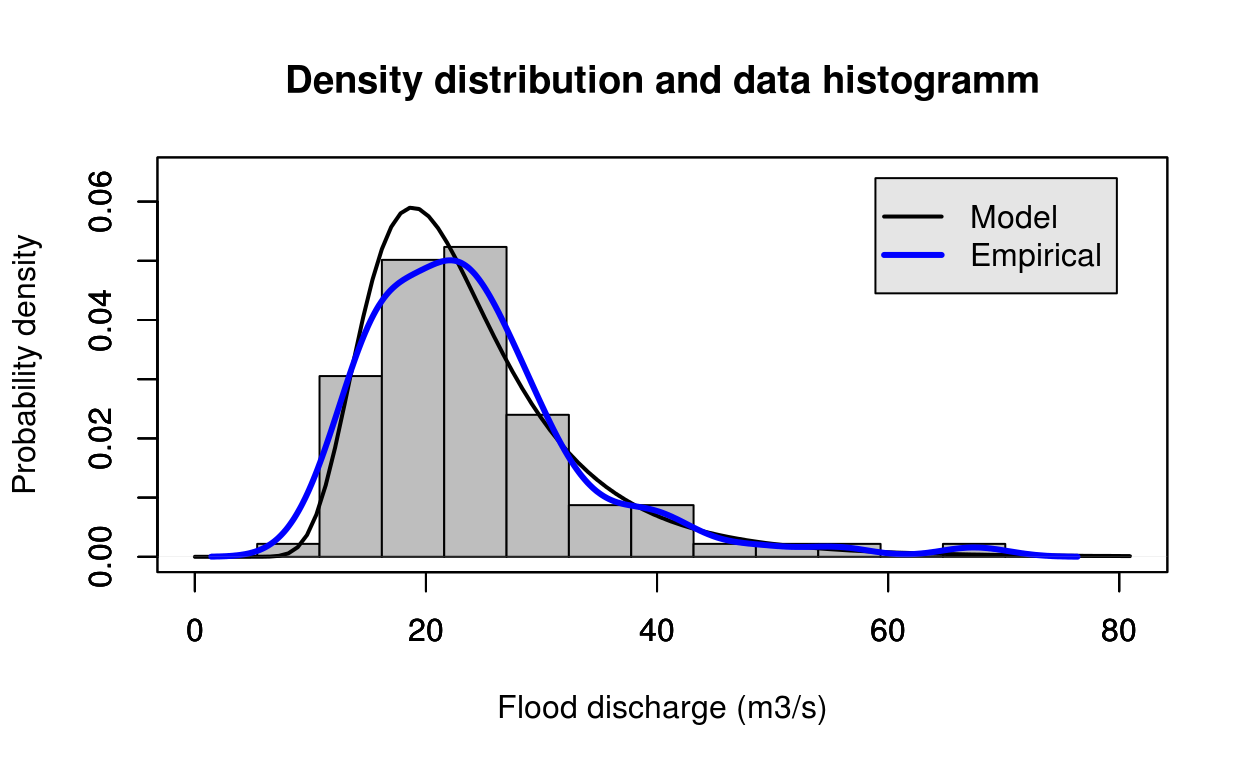

See also

gev_Lmom, gev_mom

gev_mom

Fitting the GEV distribution with mom

Function to fit the GEV distribution with the ordinary moments method

Usage

gev_mom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se) Standard error is not yet implemented

Examples

library(FlomKartShinyApp)
estimate = gev_mom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 3)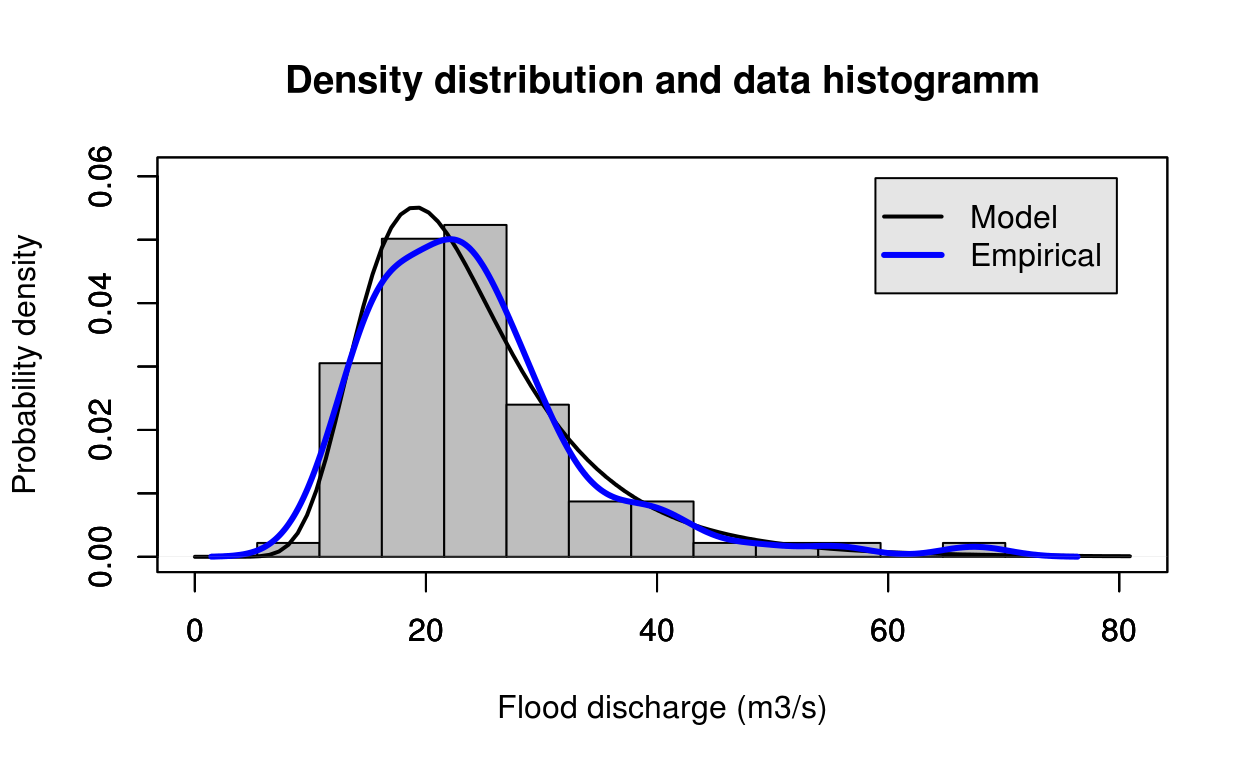

See also

gev_Lmom, gev_mle

gl_bayes

Fitting the GL distribution with Bayesian inference

Function to fit the Generalized Logistics distribution with BayesianMCMC method We assume that the shape parameter only has a prior with mean zero and standard deviation 0.2 (dnorm(x[3], 0, 0.2))

Usage

gl_bayes(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gl_bayes(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 4)

## Warning in log(1 - k * (x - xi)/alfa): NaNs produced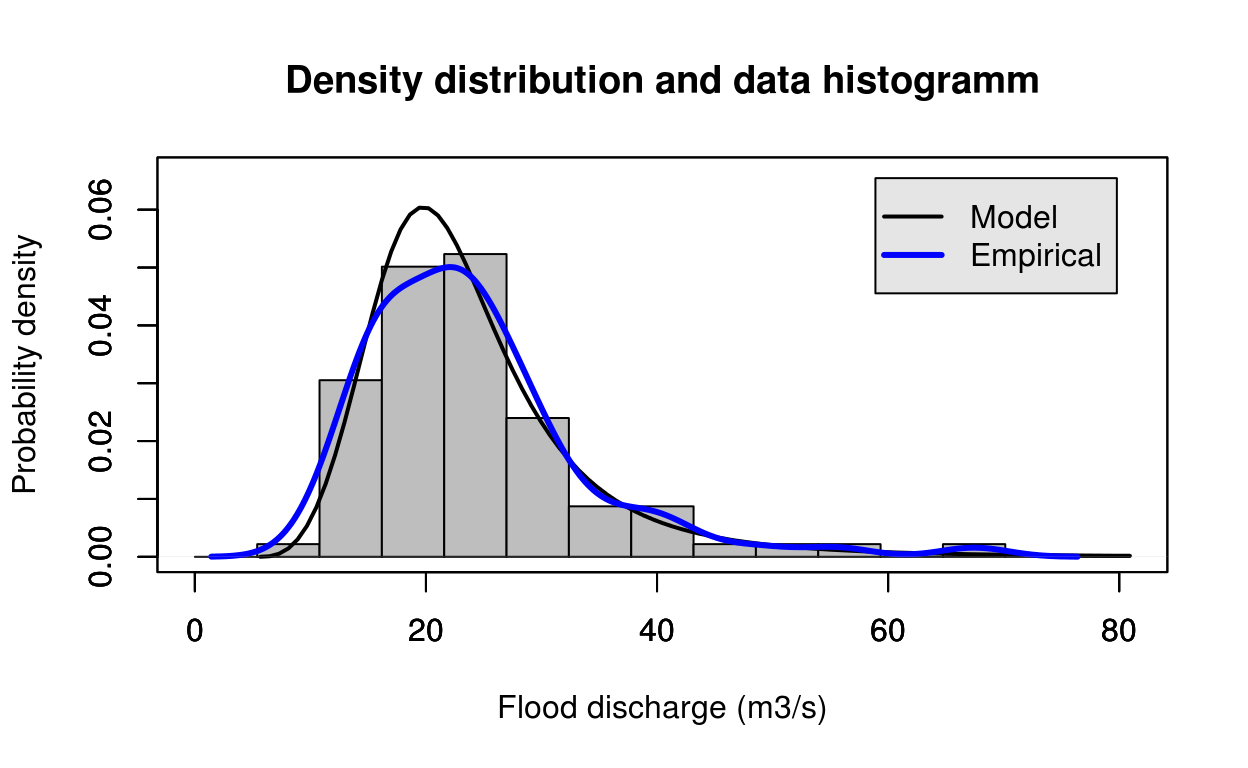

gl_Lmom

Fitting the GL distribution with Lmom

Function to fit the Generalized Logistics distribution with the linear moments method

Usage

gl_Lmom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gl_Lmom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 4)

## Warning in log(1 - k * (x - xi)/alfa): NaNs produced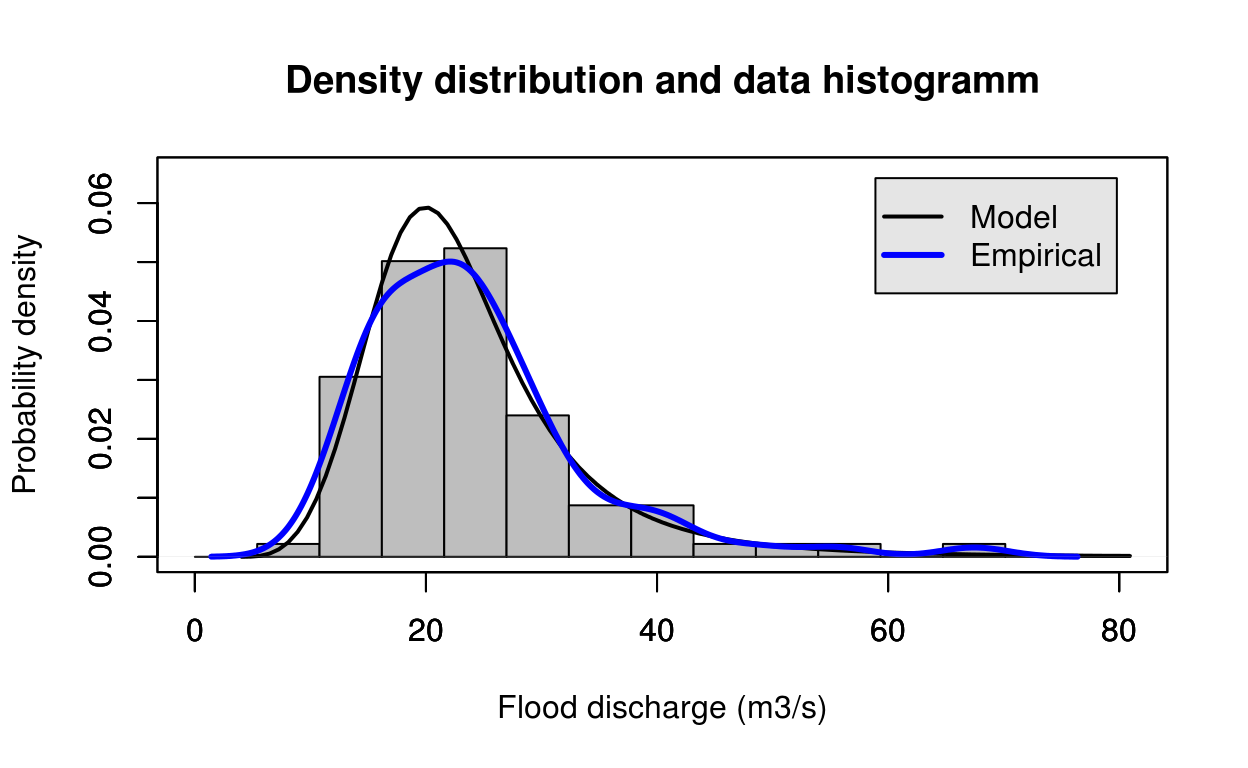

gl_mle

Fitting the GL distribution with MLE

Function to fit the GL distribution with the maximum likelihood method. This function was copied from Kolbjorn’s initial file

Usage

gl_mle(xdat, ydat = NULL, mul = NULL, sigl = NULL, shl = NULL, mulink = identity, siglink = identity, shlink = identity, muinit = NULL, siginit = NULL, shinit = NULL, show = FALSE, method = "Nelder-Mead", maxit = 10000, ...)

Arguments

…

Function to fit the GL distribution with the maximum likelihood method. This function was copied from Kolbjorn’s initial file

Value

param Estimated parameters and standard error returned as a list($estimate, $se) Standard error is not yet implemented

Examples

library(FlomKartShinyApp)
estimate = gl_mle(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 4)

## Warning in log(1 - k * (x - xi)/alfa): NaNs produced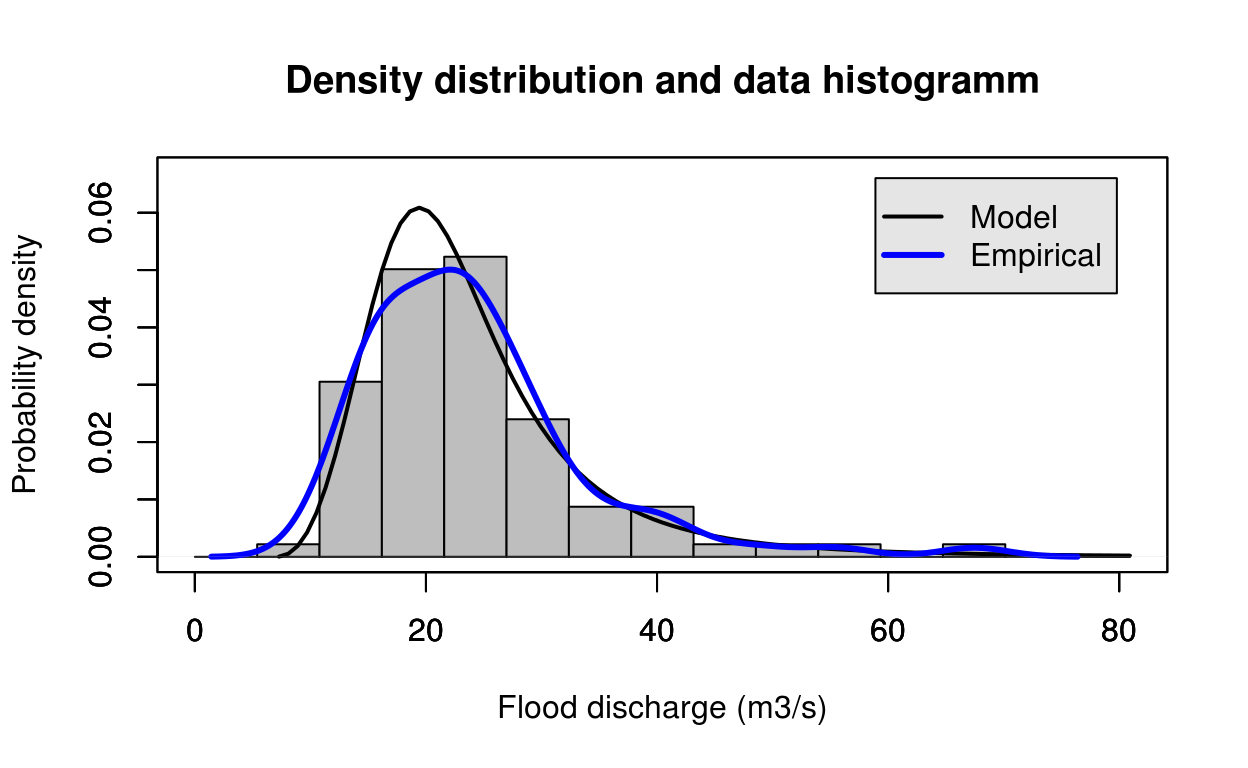

gl_mom

Fitting the GL distribution with mom

Function to fit the Generalized Logistics distribution with the ordinary moments method

Usage

gl_mom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se). Standard error is not yet implemented

Examples

library(FlomKartShinyApp)
estimate = gl_mom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 4)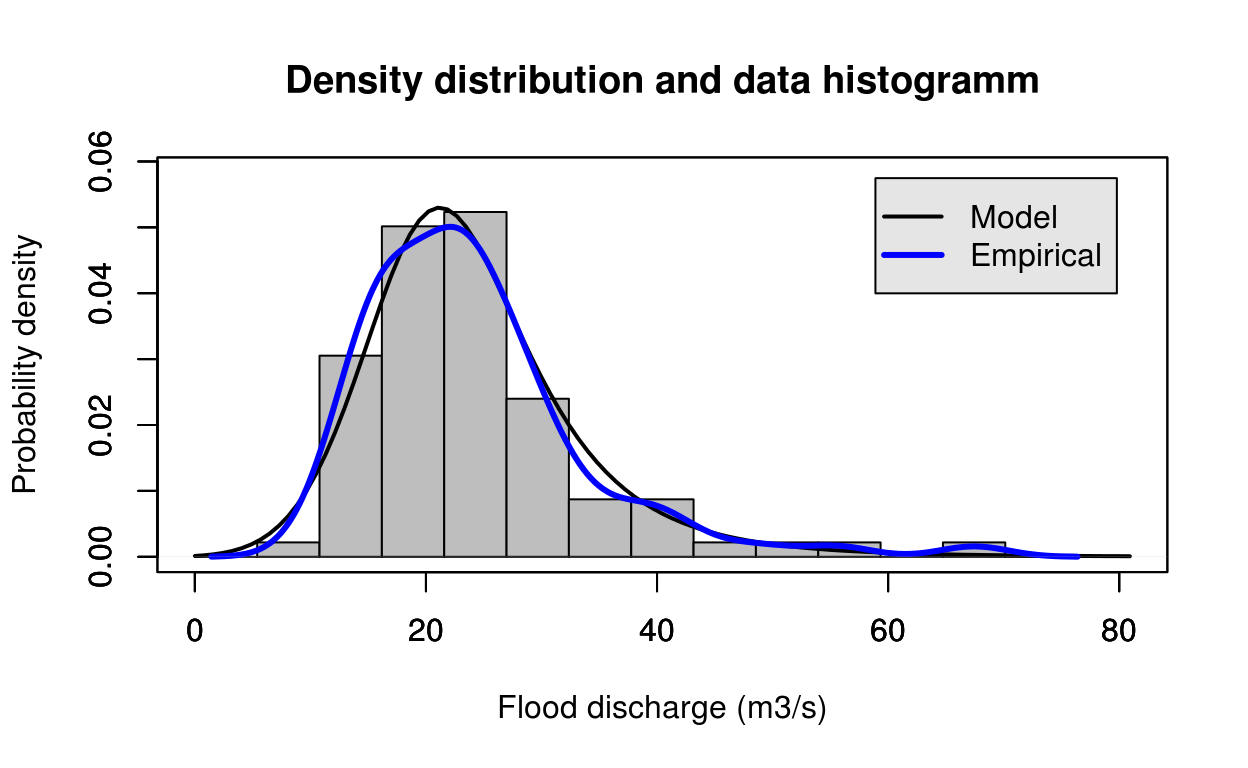

gumbel_bayes

Fitting the Gumbel distribution with Bayesian inference

Function to fit the Gumbel distribution with BayesianMCMC method We do not provide a prior for the BayesianMCMC function

Usage

gumbel_bayes(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gumbel_bayes(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 1)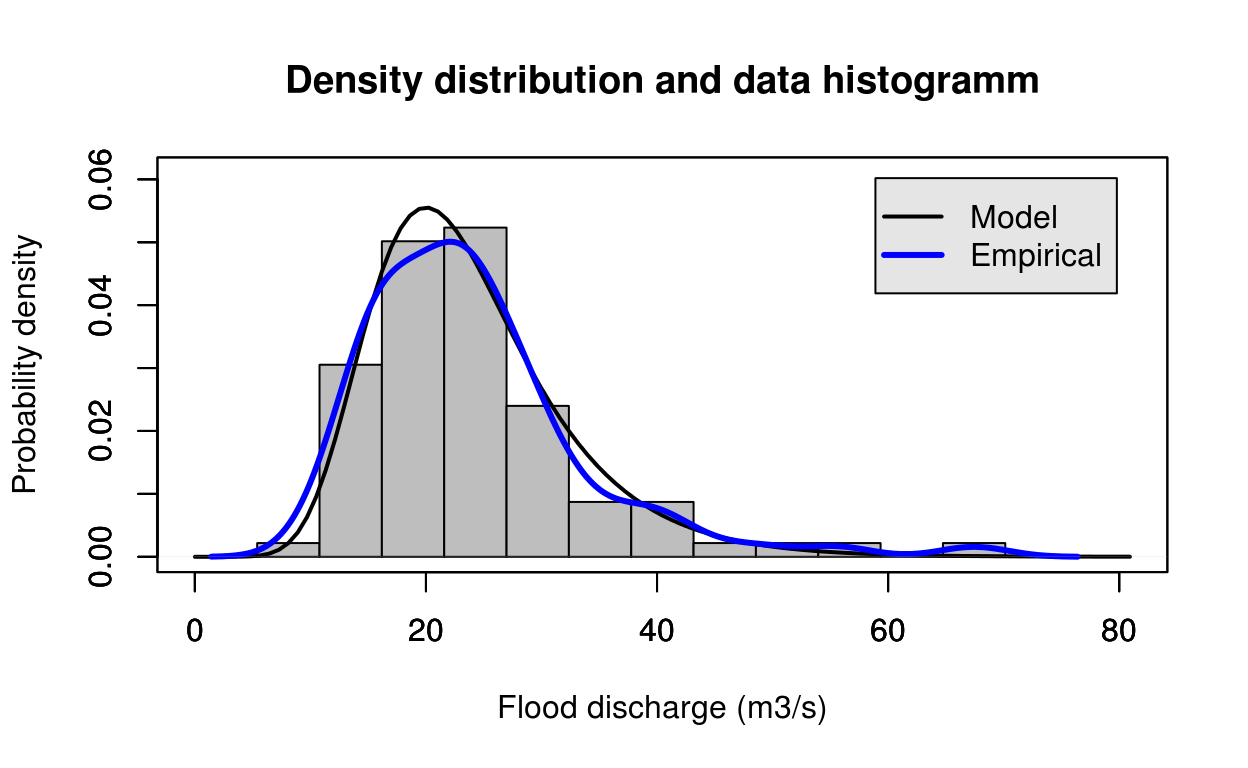

gumbel_Lmom

Fitting the Gumbel distribution with Lmom

Function to fit the Gumbel distribution with the linear moment method

Usage

gumbel_Lmom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters (2) and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gumbel_Lmom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 1)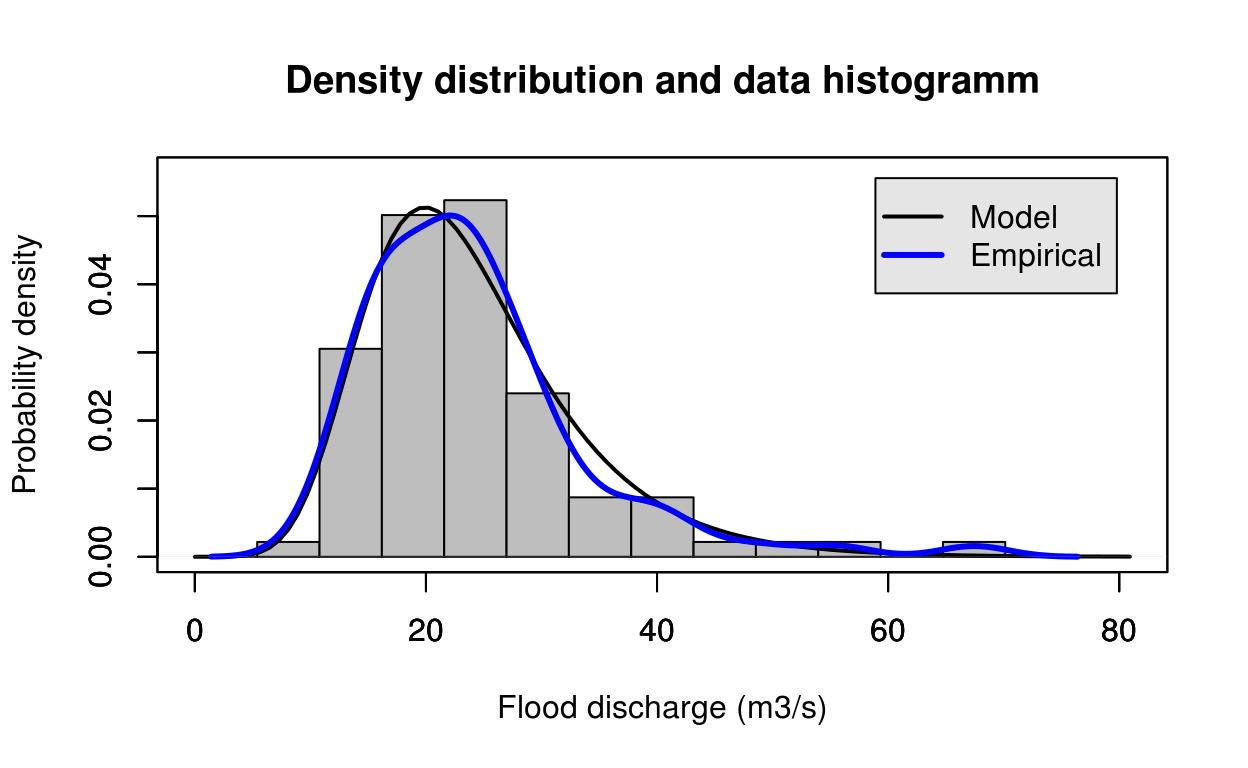

gumbel_mle

Fitting the Gumbel distribution with MLE

Function to fit the Gumbel distribution with the maximum likelihood method

Usage

gumbel_mle(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters (2) and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gumbel_mle(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 1)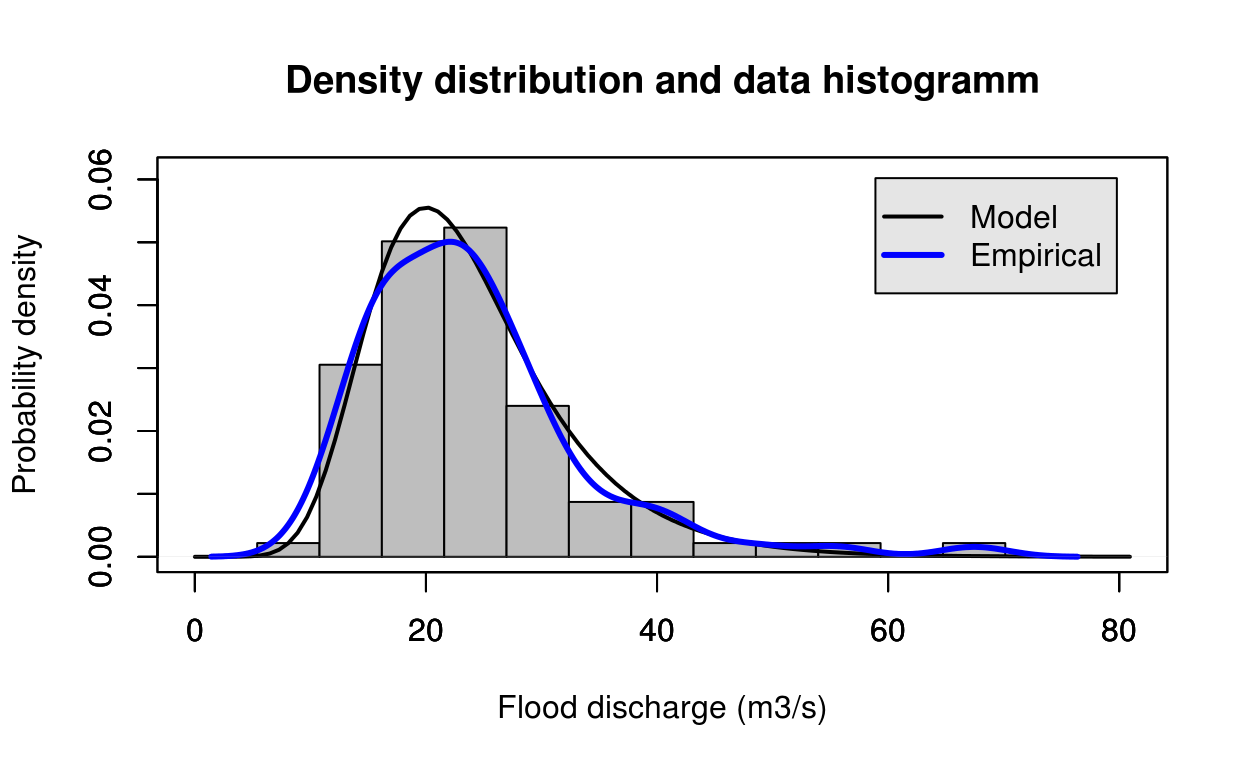

gumbel_mom

Fitting the Gumbel distribution with mom

Function to fit the Gumbel distribution with the ordinary moments method

Usage

gumbel_mom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters (2) and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = gumbel_mom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 1)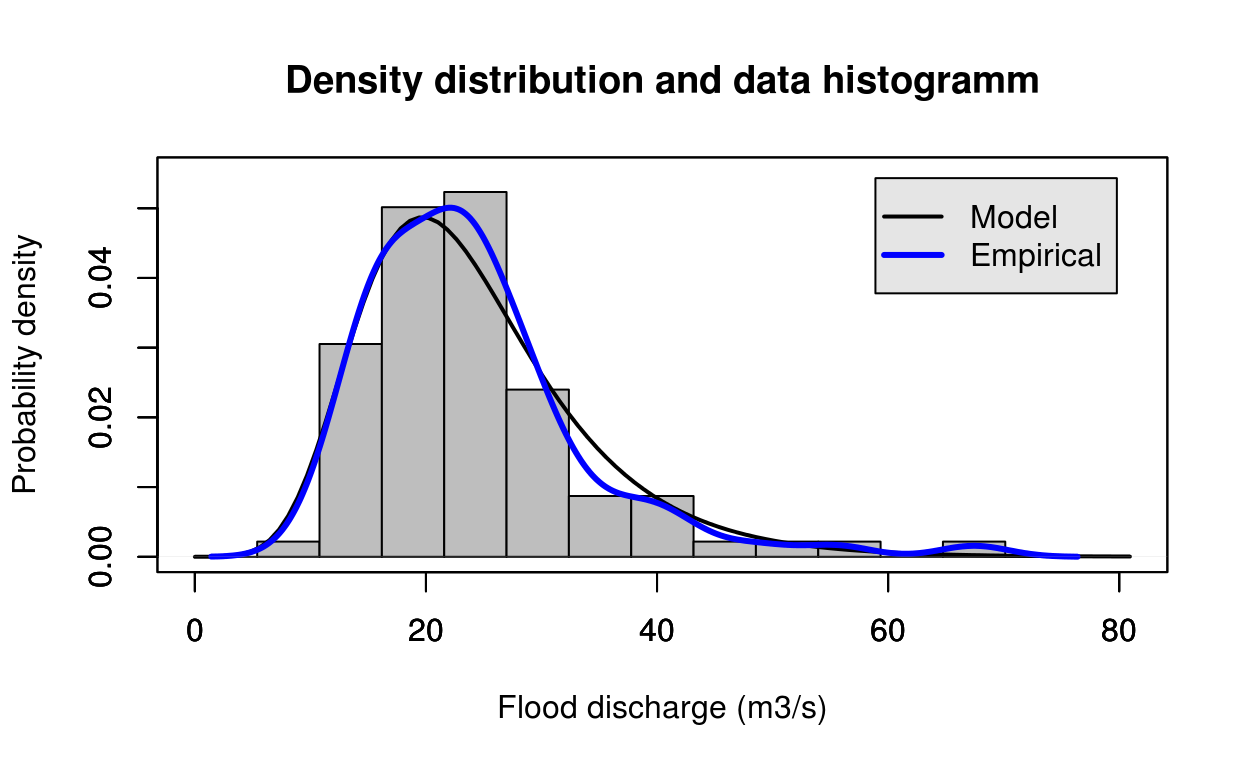

pearson_bayes

Fitting the pearson distribution with Bayesian inference

Function to fit the pearson distribution with BayesianMCMC method WE assume that the shape parameter only has a prior with mean zero and standard deviation 0.2 (dnorm(x[3], 0, 0.2))

Usage

pearson_bayes(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = pearson_bayes(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 5)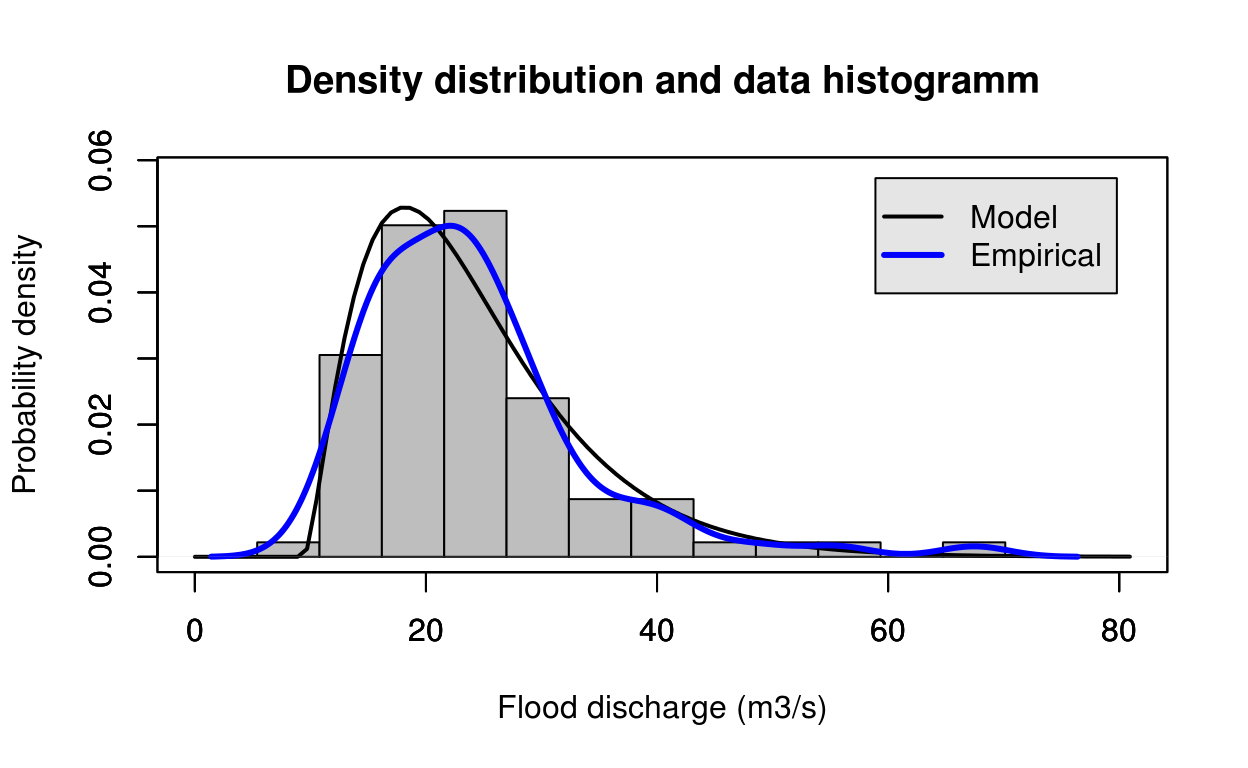

pearson_Lmom

Fitting the pearson distribution with Lmom

Function to fit the pearson distribution with the linear moment method

Usage

pearson_Lmom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se). Standard error is not yet implemented

Examples

library(FlomKartShinyApp)
estimate = pearson_Lmom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 5)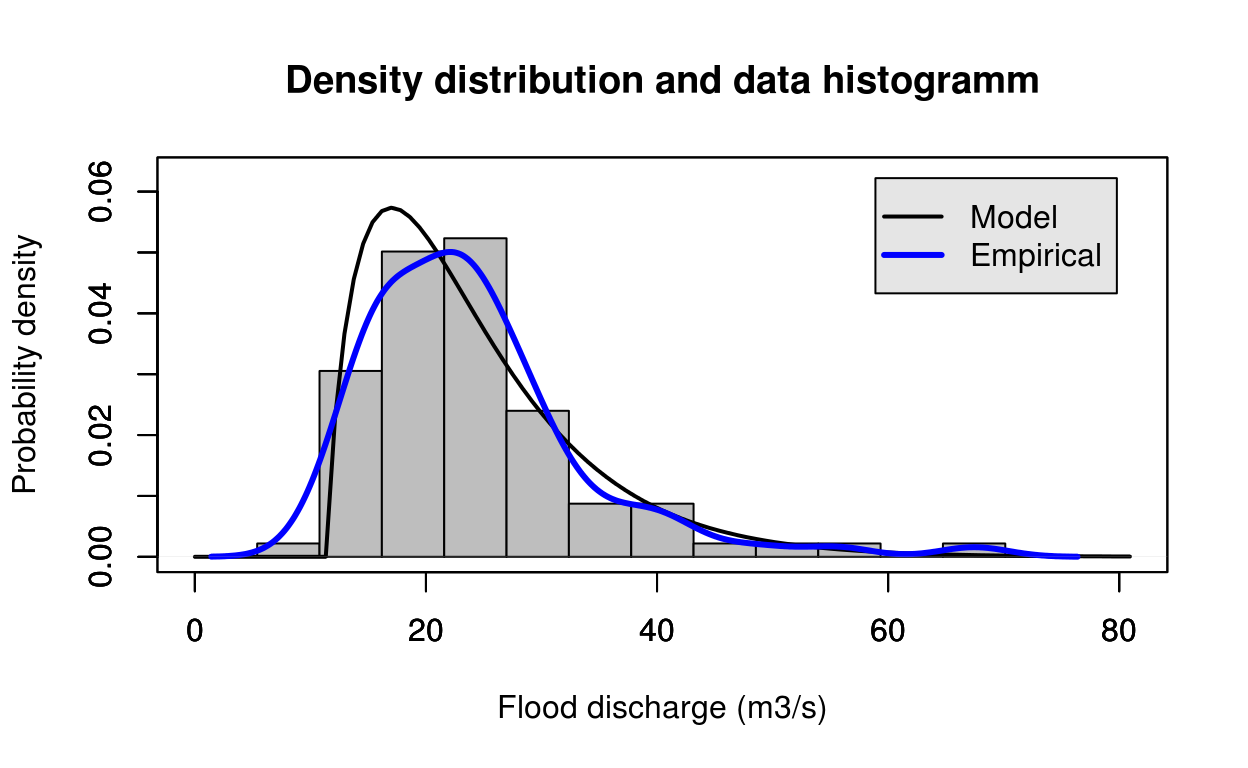

pearson_mle

Fitting the pearson distribution with MLE

Function to fit the pearson distribution with the maximum likelihood method

Usage

pearson_mle(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se)

Examples

library(FlomKartShinyApp)
estimate = pearson_mle(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 5)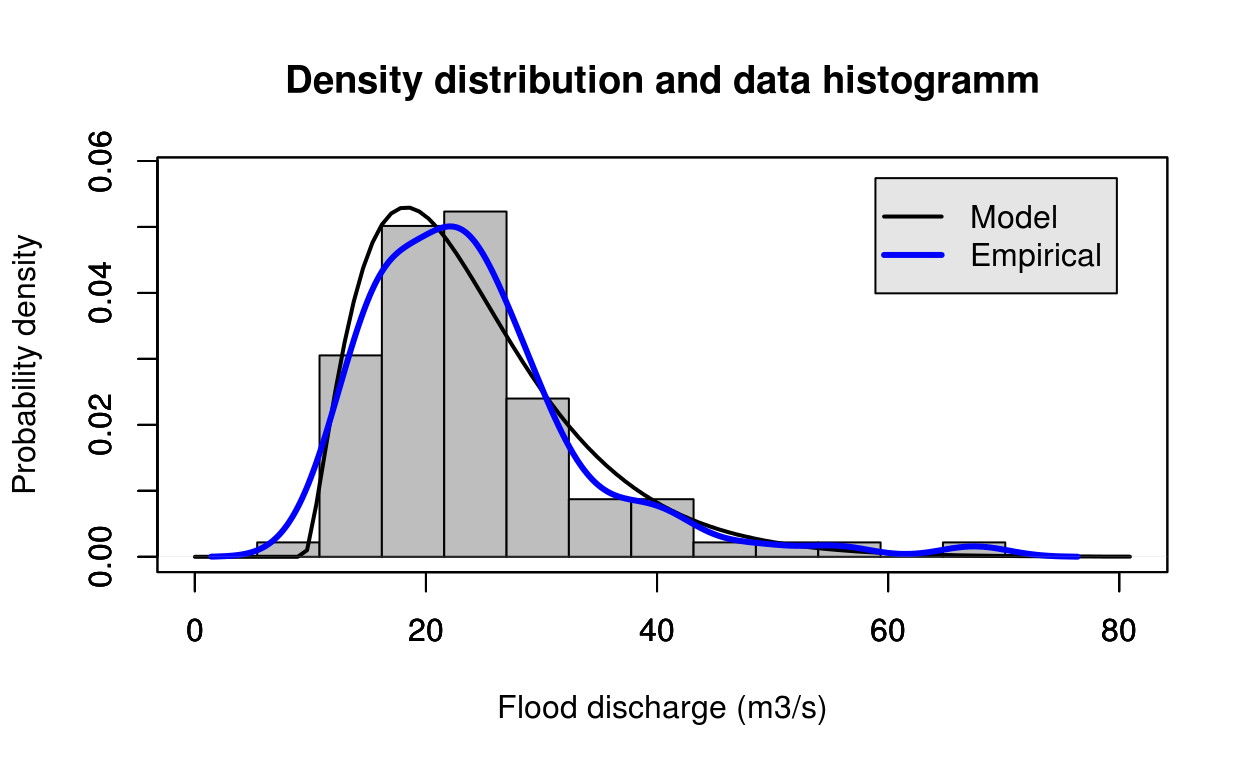

pearson_mom

Fitting the pearson distribution with mom

Function to fit the pearson distribution with the ordinary moments method

Usage

pearson_mom(dat)

Arguments

dat

the data that needs fitting (i.e. flood data)

Value

param Estimated parameters and standard error returned as a list($estimate, $se) Standard error is not yet implemented

Examples

library(FlomKartShinyApp)
estimate = pearson_mom(test_data)
FlomKartShinyApp::plot4server(test_data, param = estimate$estimate, distr = 5)